Are the intuitions related to negative utilitarianism mathematically contradictory, absurd? No. What happens is that to represent these intuitions we need more advanced mathematics than the ones we usually use. But shouldn’t an experience of negative value be canceled with another positive one of the same module or absolute value? No. That’s one way of understanding experiences, but there are other frameworks where positive and negative experiences don’t cancel each other out. But, at least you will accept that if an experience is negative, even if it is very small, as long as its value is not zero, there must be an (extraordinarily large) amount of those annoyances, such as the annoyance of a speck of dust in the eye, that accumulated must equal or exceed the suffering of torture, right? No. There are mathematical frameworks that offer alternatives to this (besides lexical priority).
Representing experiences on scales
It is common to represent on a scale positive experiences with positive numbers, and negative experiences with negative numbers. Neutral or indifferent experiences would have zero value. Something like this:
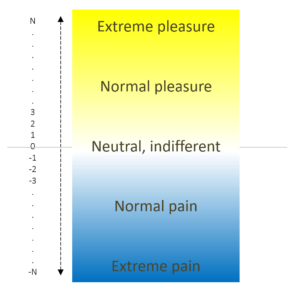
In a representation like this it seems obvious that:
- Two experiences of -5 equal one of 10 in absolute value, and therefore it seems that it would be a good idea to make a decision that leads to experiencing two experiences of -5 and one of 15, since the net balance would be 5.
- A small accumulated experience can always equal or exceed a much larger one. For example, there must be an (extraordinarily large) amount of discomfort such as the discomfort of a speck of dust in the eye, which accumulated must equal or exceed the suffering of torture.
However, these interpretations contradict some very strong intuitions about the nature of experiences. Those intuitions are:
- The intuitions of “Negative Utilitarianism” and “Tranquilism”
- The intuition that “there are experiences of a totally different nature, such as torture” or that “there are experiences of such little value that for all intents and purposes they can be considered neutral”
In particular, the second intuition can be reinforced by the long-tail effect in very negative experiences. That is, very negative experiences are very far from the range of the most common negative experiences, and in turn, there are even more negative experiences that are also very far from the range of the previous ones, etc. That is why, according to this assessment of experiences, to have an adequate view of the experiences as a whole, a logarithmic scale would be appropriate, while on the other hand, to compare two common negative experiences, the appropriate would be a common linear scale.
I am going to show some ways to describe and represent these intuitions. I believe that these representations can help a lot to understand positions in debates about moral priorities.
The intuitions of “Negative Utilitarianism” and “Tranquilism”
Negative Utilitarianism considers that the important thing is to avoid negative experiences. For negative Utilitarianism, positive experiences are good because they are not negative. For tranquilism it is enough to be well and satisfied, calm. No need to wish for more.
Under these criteria, positive and negative experiences are like sugar and salt. Sometimes it is said that salt and sugar are opposites, but the truth is that they do not act as such and do not cancel each other out. If we have made a mistake in the recipe and we have put an extra 100 grams of sugar in the cake, we will not solve it by adding 100 grams of salt to cancel it.
Bearing this intuition in mind, a more appropriate way to represent positive and negative experiences would be with two graphs, one for positive experiences, and one for negative ones, so that they are not canceled, added, or subtracted. Like sugar and salt in a cake.
The intuition that “there are experiences of a totally different nature, such as torture” or that “there are experiences of such little value that for all intents and purposes they can be considered neutral”
The annoyance of a speck of dust in the eye is extremely small, hardly noticeable. Many people share the insight that there is no cumulative amount of discomfort as small as a speck of dust in the eye that in aggregate can equate to the experience of being tortured. But it is a difficult intuition to represent because to do so we must resort to a type of mathematics to which we are generally not used.
In a summarized and simplified way, let’s say that, assuming this intuition as true, which happens is that for certain types of experience, the addition operator (+) does not behave as it usually does.
For example, we are used to 1 + 1 = 2 but in the case of experiences of magnitude as small as the experience of a speck of dust in the eye (or other even smaller ones) it could happen that the operator (+) does not add as we are used to, but it does the sums, for example, in this way:
1 + 1 = 1.5
1 + 1 + 1 = 1.75
1 + 1 + 1 + 1 = 1.875
1 + 1 + 1 + 1 + 1 = 1.9375
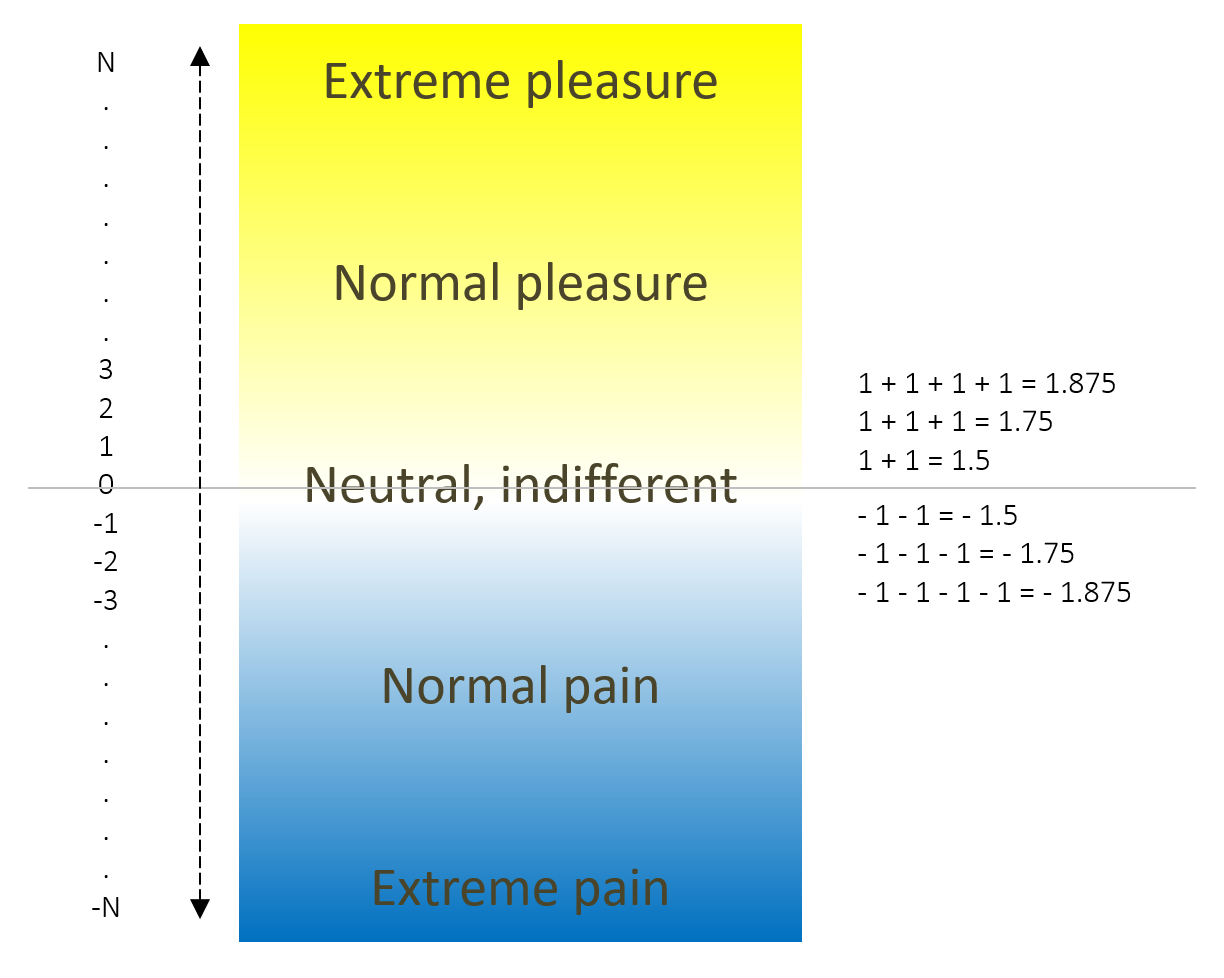
The series continues asymptotically towards the number 2 but never reaches it (1 1.5 1.75 1.875 1.9375 1.96875 1.984375 1.9921875 1.99609375 1.998046875 1.999023438 1.999511719 …). In this way, no matter how much we accumulate these small experiences, it would be impossible to achieve the relevance that experiences with a valence greater than two have.
There is a well-known context that can help us understand this, which is that of utility functions, the idea of marginal utility and and the Law of Decreasing Marginal Utility. For example, suppose that bottles of water usually cost 1 euro. If we are going through a lot of heat and there is not much water available, we will surely be willing to pay 5, 10 and even 30 euros for a bottle. That is why it is not uncommon to find sellers of bottled water at exorbitant prices in remote tourist places. In such places, the water is worth that price. And indeed if we were lost in the desert and at risk of dying of dehydration, we would probably be willing to pay an even more insane price, if such a thing were possible.
But it is important to note that this happens with the first bottle. For the second bottle we may also be willing to pay a high price, but not as high as the previous one. And the same will happen with the next, the next, etc. This is because the marginal utility of each bottle decreases as we buy more bottles. In economic theory, it is considered that this idea of marginal utility is what explains the establishment of the market price, independent of the value that we can consider “intrinsic” of the product.
Something similar is what could happen with experiences of very small magnitude. Although each experience of the annoyance of a speck of dust, considered individually, has a certain negative value, what this intuition tells us is that this negative value is less as it is added. It is very important to note that this occurs (or can occur) both for a single individual and for several individuals. That is to say:
- If a single individual experiences a sensation of -1 ten times, the sum of these experiences is not -10 but a lower number.
- If ten different individuals experience a sensation of -1 each, the total moral relevance of all these experiences grouped together is not -10 but a lower number.
This second variant of intuition may seem somewhat more difficult to believe, but in my opinion both are equally easy or difficult to believe.
The reason that the first version seems easier to believe is that we can assume that there is some kind of mechanism that plays down the specks of dust as they occur. For example, a person can get used to specks of dust, so that they bother him less and less. But this contradicts the approach of the matter, since, in my opinion, the real dilemma is about accumulating “the subjective experience of the annoyance of a speck of dust” and not simply “specks of dust” in the eye.
Non linearity and non Archimedean utilities
Regarding the mathematical tools that can represent these intuitions, and in Louis Brown‘s words:
“Namely, I don’t think there’s any number we can increase 3^^^3 to that would change the answer, because I think the disutility of dust specks is fundamentally incomparable with that of torture. If you disagree with me, I don’t care–that’s not actually the point of this post. Below, I’ll introduce a generalized type of utility function which allows for making this kind of statement with mathematical rigor.
…
Archimedean utility function necessarily yields some number of dust specks to which torture is preferable. One resolution is to reject linearity: very smart people have discussed this at length. There is another option though which, as far as the author can tell, hardly ever gets proper attention: rejecting Archimedean utilities.
…
I think many LW folk (and almost all non-philosophers) are firm dusters and have felt dismayed at their inability to justify this within Archimedean utility theory, or have thrown up their hands and given up linearity believing it to be the only option. While we will never encounter a world with 3^^^3 people in it to be dusted, it’s important to understand the subtleties of how our utility functions actually work, especially if we would like to use them to align AI who will have vastly more ability than us to consider many small utilities and aggregate them in ways that we don’t necessarily believe they should.”
References
- Logarithmic Scales of Pleasure and Pain: Rating, Ranking, and Comparing Peak Experiences Suggest the Existence of Long Tails for Bliss and Suffering.
- Lexical views without abrupt breaks (weak lexicality, weak superiority and weak inferiority)
- Torture vs. Dust Specks (at lesswrong).
- Torture vs. Dust Specks (at greaterwrong). In comments we can read that something can be “qualitatively worse”. Other comments speak of “valuing money at more utility per dollar when you have less money and less utility per dollar when you have more money” or “There isn’t enough matter in the universe to make that many dust specks, let alone the eyes to be hit and nervous systems to experience it”.
- Torture vs Dust Specks Yet Again.
- Jews and Nazis: a version of dust specks vs torture.
- Torture and Dust Specks and Joy–Oh my! or: Non-Archimedean Utility Functions as Pseudograded Vector Spaces (non linearity, non Archimedean utilities).
- Why I’m Not a Negative Utilitarian (The pinprick argument).
- Thoughts on Ord’s “Why I’m Not a Negative Utilitarian” (Thresholds and pinpricks).
- Value lexicality.
- Value superiority. A PhD Philosophy Research Proposal. (“that virtue is better than any amount of pleasure” … “that torture is worse than any amount of mild headaches” … “These ideas have been discussed under the labels “higher goods,” “higher values,” “value superiority,” “discontinuity,” “trumping” and “lexicality.””).
- Debate about Consequentialism, Pinprick Argument, the World Destruction Argument at The Hedonistic Imperative.
- What are the best arguments for an exclusively hedonistic view of value?
- Asymmetries and compensations between pleasure and pain
- The Problem of Pain, by C.S. Lewis. (“Suppose that I have a toothache of intensity x: and suppose that you, who are seated beside me, also begin to have a toothache of intensity x. You may, if you choose, say that the total amount of pain in the room is now 2x. But you must remember that no one is suffering 2x”)
- Value lexicality and Measuring happiness and suffering from Simon Knutsson
Note: To illustrate the case of very small negative experiences, the different authors speak of experiences such as: that of a speck of dust in the eye (dust specks), pinpricks (or pin pricks or pin-pricks, or just pricks), or mild headaches.
Motivation
The debate presented here is frustrating and generates interest, in my opinion, perverse. The reason for the frustration I think is, as Louis Brown points out, that individuals have very strong different intuitions and yet they do not have the tools to represent and express them. This generates, in my opinion, a great frustration, which reminds me of the frustration of trying to pronounce a well-known word correctly when we have part of the mouth anesthetized. The attempt to break free from this frustration is what I think fuels this debate.
I have never given an answer to this debate, neither in public nor in my head, until now. Although I am of the heuristic opinion (in the form of “Rule of thumb“) that reducing intense suffering takes precedence over reducing minor suffering, I am aware that this is a very crude rule that will be inappropriate in countless situations. Since I had a first encounter with this issue, I have avoided participating in it until I have a mathematical way of expressing the possibility that the sum of small quantities cannot equal a larger one. All this time I have thought that once well defined, and with the right tools, the conclusions are obvious and the debate loses all interest.
In other words, I have not had the motivation to approach this debate. Rather, to get away from him. But there is motivation to find the tools to define it well.
Years ago I was thinking about it and doing some searching, but I didn’t find anything interesting. Just before writing this text I was preparing some slides for a talk at the Day for the end of Speciesism (WoDES) on “How to recognize and demonstrate the capacity to feel“, in which I included various definitions of the concepts of sentience, consciousness and subjectivity, and spoke of three types of experiences: positive, negative, and neutral (or indifferent). Rehearsing the talk with the slides, I mentioned (to myself, speaking to the wall) the possibility that neutral or indifferent experiences did not exist and really all experiences were necessarily positive or negative, although perhaps of such little value that at all the effects were negligible. I remembered then that the idea of ”experiences of such small value that for all intents and purposes are negligible” is a controversial idea that requires mathematical tools that I did not have. But also these days and while I was resting I was watching some videos of quantum physics and the description of gravity as a field and not as a force, so that objects behave differently depending on where they are.
Somehow I connected both things and came to the conclusion that the sum (+) operator should behave differently depending on the area in which we are in the space of suffering, and it occurred to me to illustrate it with an asymptote from 1 to 2. Only after writing it down and looking for references did I come across the mention of non-linearity and non-Archimedean utilities by Louis Brown, who I think is the one who has definitely cleared the whole thing up.
Intention
The objective of this text is to offer the reader an up-to-date overview of this debate, as well as some tools to address it.
Acknowledgments
I appreciate the suggestions received from Michael St. Jules.
1 Comment